In order to simulate in a very versatile way a wide range of two-dimensional fluid-structure interaction problems involving rigid hyper-elastic materials, a fully Eulerian method has been developed. The geometry of the structure is followed implicitly through the level-set formalism (through a signed distance function), which enables the definition of a diffuse fluid-structure interface. We get use of the non-linear two-parameter Mooney-Rivlin model, which is particularly relevant to describe the behavior of materials undergoing from moderate to large deformations. The rigid part, for which the position and velocities are defined beforehand, is taken into account via a penalization term. A unified single-continuum model is solved monolithically using a Finite Volume method on quadtree-type hierarchical Cartesian meshes. This approach provides a good trade-off between the numerical accuracy and the feasibility of the simulation of the multi-physics problem, especially thanks to the dynamic mesh adaptation AMR process. The construction of the discretization schemes in space is based on the use of compact stencils, which guarantees an optimal efficiency of the parallelism.
The numerical method has been validated with respect to the literature and the benefit obtained in terms of computational costs through the use of dynamic adaptive meshes has been highlighted. Using the one-dimensional asymptotic analysis of the discretization scheme, a stabilization of the Finite Volume method has been performed in order to improve its robustness, in particular for a better consideration of very stiff materials. The simulation of a two-dimensional axisymmetric flow in a cardiac assist device (LVAD geometry) has been carried out as a biomedical application.
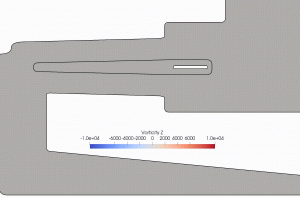
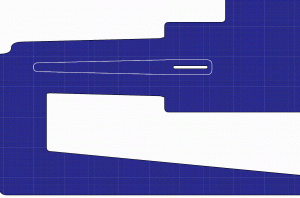
Oscillating membrane immersed in a 2D axisymmetric cardiac pump (LVAD) geometry.
Left: z-vorticity; right: adaptive grid