Authors : Hélène Barucq, Nathan Rouxelin (Former PhD student of Makutu), Sébastien Tordeux
Article published in : Low-order Prandtl-Glauert-Lorentz based Absorbing Boundary Conditions for solving the convected Helmholtz equation with Discontinuous Galerkin methods, Journal of Computational Physics, Volume 468, 2022, (link to the journal)
Many wave propagation problems are set in unbounded domain. To perform numerical simulations, it is required to truncate this domain to obtain a finite computational region that can be handled by computers.
The two most popular domain truncation techniques are
- Perfectly Matched Layers (PML): a layer of absorbing material is added outside the domain of interest, here perfectly matched means that no reflection should appear at the interface between the physical domain and absorbing layer,
- Absorbing Boundary Conditions (ABC): the physical domain is surrounded by an artificial boundary on which a non-reflecting boundary conditions is enforced, when the dimension of the domain is greater than one, exact ABCs are non-local and devising local approximation of those ABCs is a challenging problem.
For the convected Helmholtz equation, stable PMLs have been devised, but they are difficult to use with numerical methods belonging to the family of mixed finite-elements, such has Hybridizable Discontinuous Galerkin (HDG) methods.
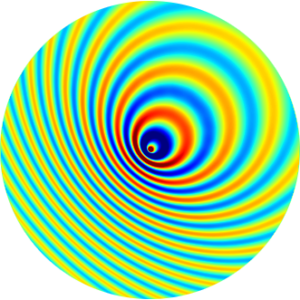
In this work, we introduce a simple way to construct ABCs for the convected Helmholtz equation from the ABCs formerly derived for the standard Helmholtz equation. This leads to local ABCs that are efficient and easy to implement.
As for the derivation of stable PMLs for the convected Helmholtz equation, the main tool of this work is the Prandtl-Glauert-Lorentz transformation which transforms the convected Helmholtz equation to the standard Helmholtz equation.
Some numerical results