Pose from Direct Linear Transform method

Introduction

Although PnP is intrinsically a non-linear problem, a sim- ple solution known as Direct Linear Transform (DLT) [3] [5] based on the resolution of a linear system can be considered.

Source code

The following source code also available in pose-dlt.cpp allows to compute the pose of the camera from points.

Source code explained

First of all we include the header of the files that are requested to manipulate vectors and matrices.

Then we introduce the function that does the pose estimation. It takes as input parameters 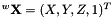the 3D coordinates of the points in the world frame and 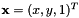their normalized coordinates in the image plane. It returns the estimated pose as an homogeneous matrix transformation.

The implementation of the Direct Linear Transform algorithm is done next. First, for each point we update the values of matrix A using equation (5). Then we solve the system Ah=0 using a Singular Value Decomposition of A. Finaly, we determine the smallest eigen value that allows to identify the eigen vector that corresponds to the solution.

From now the resulting eigen vector h that corresponds to the minimal eigen value of matrix A is used to update the homogenous transformation cTw:

Finally we define the main() function in which we will initialize the input data before calling the previous function and computing the pose using DLT algorithm.

First in the main() we create the data structures that will contain the 3D points coordinates wX in the world frame, their coordinates in the camera frame cX and their coordinates in the image plane x obtained after prerspective projection. Note here that at least 4 non coplanar points are requested to estimate the pose.

For our simulation we then initialize the input data from a ground truth pose cTw_truth. For each point we set the values (cX, cY, cZ) corresponding to the 3D coordinates of the points in the camera frame and their coordinates (x, y) in the image plane.

From here we have initialize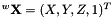d and 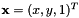. We are now ready to call the function that does the pose estimation.

Resulting pose estimation

If you run the previous code, it we produce the following result that shows that the estimated pose is equal to the ground truth one used to generate the input data:

cTw (ground truth):
0.7072945484  -0.706170438  0.03252282796  0.1  
0.706170438  0.7036809008  -0.078463382  0.1  
0.03252282796  0.078463382  0.9963863524  1.2  
0  0  0  1  
cTw (computed with DLT):
0.7072945484  -0.706170438  0.03252282796  0.1  
0.706170438  0.7036809008  -0.078463382  0.1  
0.03252282796  0.078463382  0.9963863524  1.2  
0  0  0  1