Introduction

The estimation of an homography from coplanar points can be easily and precisely achieved using a Direct Linear Transform algorithm [3] [5] based on the resolution of a linear system.

Source code

The following source code also available in homography-dlt.cpp allows to estimate the homography between matched coplanar points. At least 4 points are required.

Source code explained

First of all we inlude the header of the files that are requested to manipulate vectors and matrices.

Then we introduce the function that does the homography estimation.

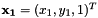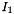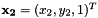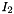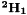From a vector of planar points ${\bf x_1} = (x_1, y_1, 1)^T$ in image $I_1$ and a vector of matched points ${\bf x_2} = (x_2, y_2, 1)^T$ in image $I_2$ it allows to estimate the homography $\bf {^2}H_1$ :

$\bf x_2 = {^2}H_1 x_1$

The implementation of the Direct Linear Transform algorithm to estimate 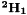$\bf {^2}H_1$ is done next. First, for each point we update the values of matrix A using equation (33). Then we solve the system 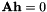${\bf Ah}=0$ using a Singular Value Decomposition of 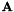$\bf A$ . Finaly, we determine the smallest eigen value that allows to identify the eigen vector that corresponds to the solution $\bf h$ .

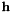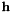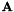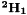From now the resulting eigen vector $\bf h$ that corresponds to the minimal eigen value of matrix $\bf A$ is used to update the homography $\bf {^2}H_1$ .

Finally we define the main() function in which we will initialize the input data before calling the previous function.

First in the main() we create the data structures that will contain the 3D points coordinates wX in the world frame, their coordinates in the camera frame 1 c1X and 2 c2X and their coordinates in the image plane x1 and x2 obtained after perspective projection. Note here that at least 4 coplanar points are requested to estimate the 8 parameters of the homography.

For our simulation we then initialize the input data from a ground truth pose c1Tw_truth that corresponds to the pose of the camera in frame 1 with respect to the object frame. For each point, we compute their coordinates in the camera frame 1 (c1X, c1Y, c1Z). These values are then used to compute their coordinates in the image plane (x1, y1) using perspective projection.

Thanks to the ground truth transformation c2Tc1 between camera frame 2 and camera frame 1, we compute also the coordinates of the points in camera frame 2 (c2X, c2Y, c2Z) and their corresponding coordinates (x2, y2) in the image plane.

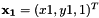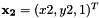From here we have initialized ${\bf x_1} = (x1,y1,1)^T$ and ${\bf x_2} = (x2,y2,1)^T$ . We are now ready to call the function that does the homography estimation.

Resulting homography estimation

If you run the previous code, it we produce the following result that shows that the estimated pose is equal to the ground truth one used to generate the input data:

2H1 (computed with DLT):
-0.5425233874  0.04785624324  -0.03308292557  
-0.04764480242  -0.5427592709  -0.005830349194  
0.02550335177  0.005978041063  -0.6361649707 

Table of Contents

Introduction

Source code

Source code explained

Resulting homography estimation