Compression-based inference of connectome motif sets
Physical and functional constraints on empirical networks lead to topological patterns across multiple scales. A particular type of higher-order network feature that has received considerable interest is network motifs—statistically regular subgraphs. These may implement fundamental logical or functional circuits and have thus been referred to as “building blocks of complex networks”. Their well-defined structures and small sizes furthermore mean that their function is amenable to testing in synthetic and natural experiments. The statistical inference of network motifs is however fraught with challenges, from defining the appropriate null model and sampling it to accounting for the large number of candidate motifs and their potential correlations in statistical testing. In this project, we develop a framework for motif set inference based on network compression. The minimum description length principle lets us select the most significant set of motifs as well as other prominent network features in terms of their combined compression of the network. Our aim is to overcome the common problems in mainstream frequency-based motif analysis. Our approach inherently accounts for multiple testing and correlations between subgraphs and does not rely on a priori specification of a null model. This provides a novel definition of motif significance which guarantees robust statistical inference. We contribute to comparative connectomics, by evaluating the compressibility of diverse biological neural networks, including the connectomes of C. elegans and Drosophila melanogaster at different developmental stages, and by comparing topological properties of their motifs.

Experimental and theoretical neuromodulation
The internal state of the larva – for instance, its feeding state – influences its behavior and decision-making through neuromodulation, a process by which neurotransmitters regulate the activity of neuronal populations.
We aim to understand how neuromodulation acts at the single-neuron level to alter decision-making circuits. To address this, we are conducting experiments in collaboration with the Jovanic’ Lab, focusing on circuits already known to be responsible for decision-making in Drosophila larvae, which are subject to neuromodulation (such as in sucrose feeding).
Theoretically, we investigate toy machine learning problems where artificial neural networks must perform opposite behaviors by changing only a subset of their parameters.
Here below, we consider a classifier of handwritten digits (cf. MNIST) in which a subset of parameters can take two distinct states. Depending on the current state, the model must output the correct label (0 for 0 and 1 for 1) in the first state or the inverse (0 for 1 and 1 for 0) in the second state. The network is trained to specifically rely on this informative subset to interpret both the input and its current state.
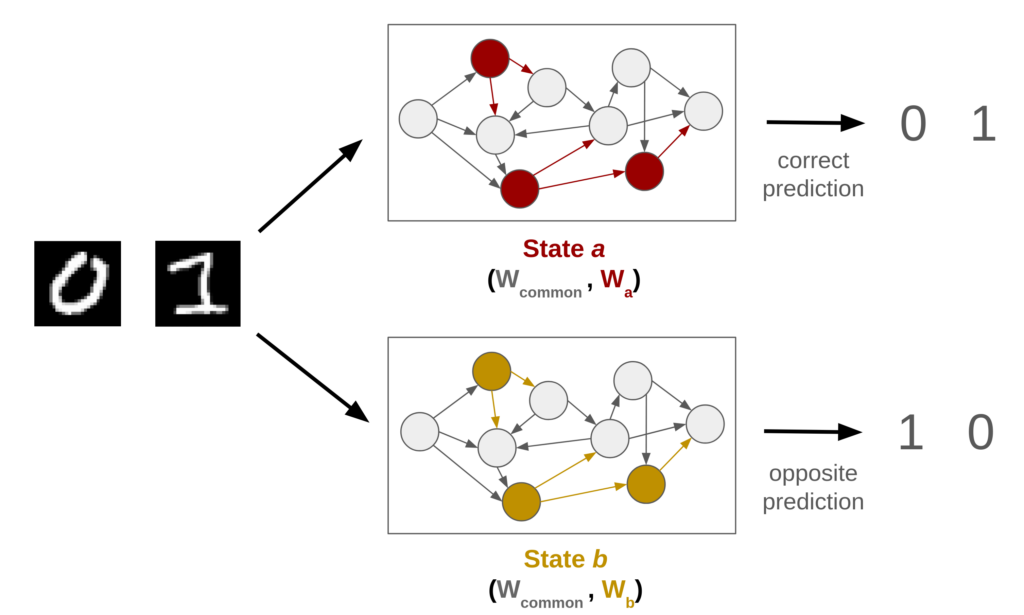
Leveraging this approach will permit to investigate the structural effects of neuromodulating bias and weight parameters in both feedforward and recurrent networks. In particular, we aim to study the impact of the number, position and type of modulated units (see below) , as well as the effects of imposing a limited budget for changes between states.

Generative latent space of the connectome
Full insect brain connectomes have recently been obtained, providing access to the complete connectivity matrix between neurons. Due to the amount of connections and possible patterns, using latent space representations is crucial to explore underlying biological properties and structures. Additionally, they hold considerable significance for extracting statistically relevant features from connectomes, which are generally obtained as a single instance per species, making it challenging to establish a null model or reference.
In this project, we focus on three main points:
- Extract a low-dimensional latent representation of the connectome.
- Identify specific structures hidden in the latent space that may reveal biological properties such as underlying neural architecture or neuron types.
- By leveraging kernel functions, introduce a generative aspect to the latent space, enabling the creation of artificial connectomes with learned and tunable properties.
Below is an example of a latent space being optimized using a learnable Gaussian kernel. The underlying structure is a feedforward network with typical synaptic weights observed in the adult Drosophila brain. Each neuron is represented by two points that characterize its afferent (incoming) and efferent (outgoing) synapses. A similar results is also provided for a quad torus.
Multiplexing larva circuits
In this project, we aim to leverage specific circuit motifs commonly found in the Drosophila connectome to explore why these particular motifs are repeated and to understand their functional roles. We will investigate artificial neural structures formed by the large-scale combination/concatenation of these motifs. By examining their operating points and the robustness of their architectures under noise and competitive interactions, we aim to uncover the utility of these motifs


Here are examples of lateral and concatenation of multiplexing.



