Drosophila Larva
This project aims to probe biological decision at the level of the neural circuits. Drosophila larva is a promising neuroscience model, providing in a single animal access to full-CNS synaptic wiring, genetic manipulation and imaging of neural activity at the level of single neurons, and large-scale automated behavior experiments. Taken altogether, this allows us to causally link neural circuits and activity to decision making in the animal.
In other words, by combining automated analysis of the dynamical behavior of Drosophila larvae with both computational and experimental studies of small neural circuits involved in decision-making, we aim to uncover how such decisions are implemented.
The larva is a ~10000 neurons that exhibit complex behaviour dynamics in response to external stimuli and to possible internal states. This project is done in close collaboration with Marta zlatic’s lab at the Janelia Research Campus and Jovanic’s lab at NeuroPSI.
A first step is to develop a reliable action detection algorithm. Nearly ~500 000 larvae have been recorded. Here, we show a video example showing a larva behavioural dynamics. Color of the larva is associated to the action being performed. Black for run, Red for casting and turning, green for stoping, deep blue for hunching (a defensive action characterised by fast diminution of length)
The second is link neural activation and inactivating to action and sequences of action selections. Here, we show an example of diagram showing the derivative of the probability of actions immediately after an air puff (the Jovanic Screen ). Every line is a neuron or a set of neurons being silenced. Color code is associated to amplitude with deep cyan for strong decrease (negative values) and with deep pink for strong increase.
The third was to observe larva decision in complex environments. We rely on a closeloop setup where z larva is optogenetically stimulated during specific behaviors. We are investigating decision-making during ambiguous stimuli, where rapid decisions must be made. Here, we present an example of a ‘game’ in which side-dependent nociceptive stimuli are associated with casting events. Note the numerous head casts required to escape the nociceptive signal on the low-intensity side.
Phenotyping as a statistical test
A last step was to build a continuous self-supervised representation of the behaviour. We developed a continuous representation of the behaviour based on self-supervised learning (SSL) to alleviate the need for a predefined behavioural dictionary to characterize larvae actions.

Here we show: (A) the general architecture of the self-supervised predictive autoencoder. (B)
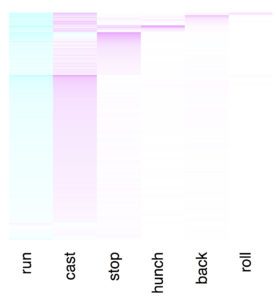
Visualization of the latent space projected in 2D using UMAP with colours corresponding to the discrete behaviour dictionary (black: crawl, red: bend, green: stop, blue: hunch, cyan: back, and yellow: roll) (C) Transition probability from one discrete state to the other as a function of the position in the latent
space: here, between run and bend.
By relying on this latent space representation it becomes feasible to tell apart different phenotype from their trajectory in the latent space. It lay groundwork to assess the effect of genotpye variability and mutations on decision directly from the observed macroscopic behavior.

Here we show an illustration of our phenotyping modelling strategy for each genotype. The behavior evolution on the experimental setup is extracted usually after the onset of the stimuli, and projected on the latent space using an encoder. The phenotype of the genotype is the distribution of all the points in the latent space regularised by a Gaussian kernel. (B) There is a correspondence between statistical testing procedures based on discrete behaviour categories with chi-squared tests and testing
procedures based on continuous behaviour with MMD. (C) Latent distributions of behaviour (regularized by a Gaussian kernel) for two distinct larva lines (C1-C2) and the resulting witness function in C3 between these two latent distributions, highlighting main behavioural differences between the lines.
Simulated Body
In our pursuit of modeling the Drosophila larva, we aim to uncover new insights into the control of deformable bodies from both neural computation and muscular implementation perspectives. By leveraging the extensive repository of data on the larva’s neural connectome, along with recordings of muscular and neural activity, as well as behavioral experiments, this project seeks to develop a physics-based 3D simulation platform that accurately replicates the motor control dynamics observed in Drosophila larvae, while capturing the essential physics of body deformation and motor dynamics.
This approach will enable us to identify key parameters for generating realistic simulations and explore numerical methods for motor control. Additionally, it will provide further constraints to investigate the crucial neural circuit parameters responsible for motion and decision-making.
Ultimately, it will pave the way for the development of imitation learning approaches aimed at understanding motion control by constraining the neural circuit parameters involved in motion and decision-making.

Here we show a segmentation of individual muscles in a Drosophila melanogaster. The raw data are presented in white, and the muscles are labeled with multiple colors, with each muscle assigned a unique color. The segmentation was performed manually, following the anterior-posterior axis.

Here, we show an example of larva simulated body on SOFA software. Coarse representation of the larva body is assumed to approximate a soft body. This mesh structure will be connected by muscles whose activity can be monitored. Cables serve as simplified representations of muscles. These cables were derived from the voxel-based segmentation (shown above) of the muscles following several cleaning and processing steps.
Probabilistic larva generative models
By leveraging an extensive repository of larval motion and trajectories, it becomes possible to generate artificial sequences of larval behavior and motion using an underlying probabilistic model. A previously trained classifier can provide access to the transition probabilities between different behaviors resulting results on artificially generated sequences of motions. These motions are generated based on past recordings tagged by our automated protocol.
By manipulating the classifier, a wider range of phenotypes, including rare cases sometimes found in mutated lines, can be generated. Similarly, it becomes possible to adjust physical features of the motion to train the classifier on a more diverse range of motions.
Here, we show an example of generated sequence tested on a previously obtained classifier. Original labels are in the top left corner. Larva outline is changed depending on the action predicted by the classifier.
Decision-making as Multi-Armed Bandit Games
Multi-armed bandit problems, which involve choosing between multiple options (or ‘arms’) to maximize rewards, are prevalent in various fields, including online recommendation systems, medical trials, and dynamic pricing.
Our goals are :
– Develop new bandit algorithms inspired by physical principles, such as entropy, first passage time, and the free energy principle, which demonstrate state-of-the-art performance in both classical and more complex bandit settings.
-Extend these algorithms to real-world applications, including drug testing and optimal disease surveillance.
-Utilize the simple functional forms provided by our algorithms to study how small neural circuits in living organisms, such as Drosophila larvae, optimize decision-making. In particular, we will focus on how these circuits implement memory acquisition and adapt decisions in response to stimuli such as air puffs, CO2, or odors.
A first step was to address the exploration-exploitation dilemma in decision-making with a focus on classical multi-armed bandit problems. This dilemma involves choosing between exploiting known options
The first step was to address the exploration-exploitation dilemma in decision-making, with a focus on classical multi-armed bandit problems. This dilemma involves balancing the choice between exploiting known options for immediate gains and exploring new options for potential long-term benefits.
We developed a new class of algorithms called Approximate Information Maximization (AIM), which leverages the principle of information maximization to provide simple analytical expressions that guide decision-making in bandit contexts. We have also demonstrated the optimality of this approach.
Here we show an illustration of the multi-armed bandit problem. At each time step t the agent chooses an action that returns a reward drawn from a distribution of unknown mean. The agent’s goal is to minimize the cumulative regret. By relying on posterior distributions of bandit values after playing both arms (b)-(c) (here arm blue has a higher probability of being the best), the agent goal is to exploit the best arm while maintaining exploration (drawing green arm).