Find all our activities in our annual reports here : radar.inria.fr
-
- Inverse models for identification of cellular ionic parameters from macroscopic signals
- Modeling of mitochondrial calcium fluxes during the cardiac cellular cycle
- Propagation of action potentials on cell networks
- Highly scalable ECG simulation with electrocardiographic lead fields
- Convergence analysis of a bidomain-bath model
Inverse models for identification of cellular ionic parameters from macroscopic signals
Traditional inverse models in cardiac electrophysiology have aimed at identifying the activation (and relaxation) order of the cardiac muscle from body surface potentials. However, many cardiac anomalies cannot be reduced to such simple parameters. Underlying the activation and “repolarization” of the cells is a complex interplay of different ion channels, each with its own dynamics. Genetic and other abnormalities express themselves in one or more of these channels. We have therefore taken several initiatives to identify the properties of the channels themselves.
Measurements with micro-electrodes can capture currents generated by a handful of cultured cells. Together with the REO team at the Inria center in Paris we have developed methods to identify properties of individual ionic currents from such measurements [28], [10].
On the level of the whole heart, two studies have attempted to identify cellular properties from surface electrocardiogram (ECG) signals [29], [11]. Ravon et al. have previously developed a method that identifies activation times as well as repolarization properties of a simplified ionic model (the Mitchell-Schaeffer model) [66], but considering only the outer surface of the heart muscle. We now evaluated the capability of this method to distinguish properties of the inner and outer surfaces, which are expected to differ importantly [29]. This turned out to be extremely challenging. Abidi et al. [11], on the other hand, demonstrated that the solution to such problems is unique even for intermediately complex ionic models such as the Beeler-Reuter [46] and Luo-Rudy I [61] models.
Thus, we found that a unique solution exists but is very hard to find in practical situations. This result suggests that further work should aim at removing confounding factors such as limitations in the volume conductor models.
Modeling of mitochondrial calcium fluxes during the cardiac cellular cycle
Mitochondria are the main regulator of the energetic cycle of cells, especially in cardiac cells, which do not wear themselves under the perpetual contraction effort of the heart. In particular, mitochondria are involved in the regulation of calcium which plays a crucial role in the propagation of cardiac action potentials. However, they are not taken into account in the ionic models that are used to perform simulations at the tissue level. The ANR MITOCARD project is a first step towards models including mitochondrial activity. We aim at modeling and reproducing experimental results that will help us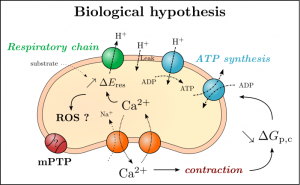 understand the interaction between mitochondria and the cells. We propose a phenomenological model of differential equations that represent main mitochondrial exchanges. This model will be calibrated with experiments, and then include mechanisms that are not or poorly taken into account in “traditional” mitochondrial models, according to IHU Liryc electrophysiologists we are working with. Read more.
understand the interaction between mitochondria and the cells. We propose a phenomenological model of differential equations that represent main mitochondrial exchanges. This model will be calibrated with experiments, and then include mechanisms that are not or poorly taken into account in “traditional” mitochondrial models, according to IHU Liryc electrophysiologists we are working with. Read more.
Propagation of action potentials on cell networks
The electrical activation of the heart relies on rapid propagation of activation impulses through intercellular connections. Cardiac arrhythmia are often due to damage to these intercellular connections. In various pathologies, loss of individual connections can lead to the formation of a complicated maze in which very slow propagation is possible, leading to reentrant arrhythmias. To investigate such phenomena, the PhD thesis work of 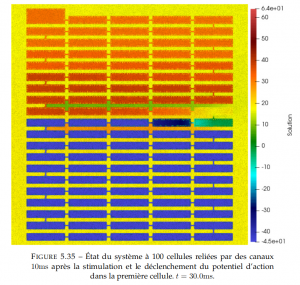 P.-E. Bécue was dedicated to the development of a three-dimensional model of the cardiac tissue with sub-cellular resolution. This work builds on our CEPS software, which was specifically extended for this purpose. Read more.
P.-E. Bécue was dedicated to the development of a three-dimensional model of the cardiac tissue with sub-cellular resolution. This work builds on our CEPS software, which was specifically extended for this purpose. Read more.
Aouadi et al. have specifically developed a model for the connections between the network of cardiac Purkinje fibers and the working myocardium. It handles the myocardium with a standard bidomain model and the Purkinje network, which consists of discrete bundles, with a one-dimensional monodomain model.
On an even smaller scale, the team also worked on a three-dimensional model of calcium release from intracellular organelles and its diffusion inside the cell.
Highly scalable ECG simulation with electrocardiographic lead fields
Currently a monodomain reaction-diffusion model is a well-established method to simulate the electrical activity of the heart [62], [63], even more so because it can be adapted to approximate a bidomain model very closely [48], [54]. Computing the electrocardiogram (ECG) from the results of such models is harder because it requires large linear systems to be solved, and does not scale well to large numbers of processors. A possible solution is to use so-called lead fields, the electrocardiographic term for a linear combination of fundamental solutions that express the ECG potential as an integral over a field of electric current dipoles. A paper published in 2018 has shown that this method gives a huge scaling advantage on highly parallel computers [27]. This result is also of practical importance for our applied work.
to be solved, and does not scale well to large numbers of processors. A possible solution is to use so-called lead fields, the electrocardiographic term for a linear combination of fundamental solutions that express the ECG potential as an integral over a field of electric current dipoles. A paper published in 2018 has shown that this method gives a huge scaling advantage on highly parallel computers [27]. This result is also of practical importance for our applied work.
Convergence analysis of a bidomain-bath model
M. Bendahmane and N. Chamakuri performed a convergence analysis for optimal control of a bidomain-bath model by using a finite-element scheme. The bidomain-bath model represents a commonly used experimental setup where a small piece of cardiac tissue is kept alive and studied for some time in a nutrient bath. The bidomain-bath model equations describe the cardiac bioelectric activity in the tissue and bath volumes where the control acts at the boundary of the tissue. The existence of the finite element scheme and convergence to a unique weak solution of the direct problem were established. The convergence proof was based on deriving a series of a-priori estimates and using a general L2-compactness criterion. Moreover, the well-posedness of the adjoint problem and the first order necessary optimality conditions were shown. Comparing to the direct problem, the convergence proof of the adjoint problem is based on using a general L1-compactness criterion. The model was used for a simulation of low-energy defibrillation.
