Contact
Inria Bordeaux Sud-Ouest
200 rue de la vieille tour 33405 Talence Cedex, France
E-mail: nejib.zemzemi@lirima.fr; mourad.bellassoued@enit.utm.tn
Nejib Zemzemi’s web page
Mourad Bellassoued’s web page
About the team
EPICARD in few words
EPICARD is an associate team between the Carmen project at Inria and “Laboratoire de Modélisation Mathématique et Numérique dans les Sciences de l’Ingénieur ” (LAMSIN). The goal of this association is to develop new mathematical approaches for solving different inverse problems in cardiac electrophysiology.
Team members
The team regroups also researchers from LAMSIN MohammedV university and from Université Technologique de Compiègne.
From Inria: Mostfa Bendahmane, Yves Coudière, Jacques Henry, Amel Karoui, Pauline Migerditichan and Nejib Zemzemi
From LAMSIN: Abir Amri, Ben Abda Amel, Rabeb Chamekh, Henda El Fekih, Fadhel Jday, Nabil Gmati Moez Kallel, Jamila Lassoued, Moncef Mahjoub
From MohamedV university: Rajae Aboulaich, El Mahdi El Guarmah, Najib Fikal and Keltoum Chahour.
From UTC de Compiègne (Laboratoire de mathématiques appliquées de Compiègne): Faker Ben Belgacem and Faten Jelassi.
Epicard fifth year achievements
Fifth year activities
Epicard fourth year achievements
Fourth year activities
Epicard second year achievements
Second year activities
Epicard first year achievements
First year activities
Scientific Production
2022
Journal articles
- titre
- Global Lipschitz stability of multiple space dependent ionic parameters for the MEA/hiPSC-CM assays
- auteur
- Hamza Ammar, Moncef Mahjoub, Nejib Zemzemi
- article
- Inverse Problems, 2022, 39 (1), pp.015010. ⟨10.1088/1361-6420/aca70d⟩
- Accès au bibtex
-
2021
Journal articles
- titre
- Cardiac Activation Maps Reconstruction: A Comparative Study Between Data-Driven and Physics-Based Methods
- auteur
- Amel Karoui, Mostafa Bendahmane, Nejib Zemzemi
- article
- Frontiers in Physiology, 2021, 12, ⟨10.3389/fphys.2021.686136⟩
- Accès au texte intégral et bibtex
-
- titre
- Analysis of the heart-torso conductivity parameters recovery inverse problem in cardiac electrophysiology ECG modelling
- auteur
- Abir Amri, Mourad Bellassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- Applicable Analysis, 2021, pp.1-30. ⟨10.1080/00036811.2021.1955861⟩
- Accès au texte intégral et bibtex
-
2019
Journal articles
- titre
- Propagation of two independent sources of uncertainty in the electrocardiography imaging inverse solution
- auteur
- Najib Fikal, Rajae Aboulaich, Emahdi El Guarmah, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2019, 14 (2), ⟨10.1051/mmnp/2018065⟩
- Accès au texte intégral et bibtex
-
- titre
- Ionic parameters identification of an inverse problem of strongly coupled PDE’s system in cardiac electrophysiology using Carleman estimates
- auteur
- Yassine Abidi, Mourad Bellassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2019, Mathematical Modelling in Cardiology, 14 (2), ⟨10.1051/mmnp/2018060⟩
- Accès au texte intégral et bibtex
-
- titre
- Towards the modelling of the Purkinje/ myocardium coupled problem: A well-posedness analysis
- auteur
- Saloua Mani Aouadi, Wajih Mbarki, Nejib Zemzemi
- article
- Journal of Computational and Applied Mathematics, 2019, ⟨10.1016/j.cam.2018.10.024⟩
- Accès au texte intégral et bibtex
-
- titre
- Analysis of the ECGI inverse problem solution with respect to the measurement boundary size and the distribution of noise
- auteur
- Mohammed Addouche, Nadra Bouarroudj, Fadhel Jday, Jacques Henry, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2019, ⟨10.1051/mmnp/2018061⟩
- Accès au texte intégral et bibtex
-
- titre
- A nash game algorithm for the solution of coupled conductivity identification and data completion in cardiac electrophysiology
- auteur
- Rabeb Chamekh, Abderrahmane Habbal, Moez Kallel, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2019, Mathematical modelling in cardiology, 14 (2), pp.15. ⟨10.1051/mmnp/2018059⟩
- Accès au texte intégral et bibtex
-
Conference papers
- titre
- Maximal conductances ionic parameters estimation in cardiac electrophysiology multiscale modelling
- auteur
- Yassine Abidi, Julien Bouyssier, Moncef Mahjoub, Nejib Zemzemi
- article
- FIMH 2019 – 10th International Conference Functionnal Imaging and Modeling of the Heart, Y. Coudière, V. Ozenne, E. Vigmond and N. Zemzemi, Jun 2019, Bordeaux, France. pp.131-138, ⟨10.1007/978-3-030-21949-9⟩
- Accès au texte intégral et bibtex
-
Preprints, Working Papers, …
- titre
- Ionic Parameters Estimation in Multi-Scale Cardiac Electrophysiology Modelling
- auteur
- Yassine Abidi, Moncef Mahjoub, Nejib Zemzemi
- article
- 2019
- Accès au texte intégral et bibtex
-
2018
Journal articles
- titre
- Evaluation of fifteen algorithms for the resolution of the electrocardiography imaging inverse problem using ex-vivo and in-silico data
- auteur
- Amel Karoui, Laura Bear, Pauline Migerditichan, Nejib Zemzemi
- article
- Frontiers in Physiology, 2018, Electrocardiographic Imaging, 9, pp.1708
- Accès au texte intégral et bibtex
-
- titre
- Numerical simulation of the fractional flow reserve (FFR)
- auteur
- Keltoum Chahour, Rajae Aboulaich, Abderrahmane Habbal, Cherif Abdelkhirane, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, In press, Special issue “Mathematical Modelling in Cardiology”
- Accès au texte intégral et bibtex
-
Conference papers
- titre
- The Heart Recording Conditions Impact the Assessment of the Electrocardiography Imaging Inverse Solution
- auteur
- Amel Karoui, Laura Bear, Pauline Migerditichan, Mostafa Bendahmane, Nejib Zemzemi
- article
- CinC 2018 – 45th Computing in Cardiology Conference, Sep 2018, Maastricht, Netherlands
- Accès au texte intégral et bibtex
-
2017
Journal articles
- titre
- Stability analysis of decoupled time-stepping schemes for the specialized conduction system/myocardium coupled problem in cardiology
- auteur
- Salwa Aouadi, W Mbarki, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2017, Mathematical models in physiology, 12 (5), pp.208-239. ⟨10.1051/mmnp/201712513⟩
- Accès au texte intégral et bibtex
-
Conference papers
- titre
- Inverse Problem of Electrocardiography: estimating the location of cardiac isquemia in a 3D geometry
- auteur
- C.E. Chavez, Nejib Zemzemi, Yves Coudière, Felipe Alonso-Atienza, Diegó Alvarez
- article
- Functional Imaging and modelling of the heart (FIMH2015), Jun 2017, Maastricht, Netherlands. ⟨10.1007/978-3-319-20309-6_45⟩
- Accès au texte intégral et bibtex
-
- titre
- New approach for solving electrocardiography imaging inverse problem with missing data on the body surface
- auteur
- Mohammed Addouche, Nadra Bouarroudj, Jacques Henry, Fadhel Jday, Nejib Zemzemi
- article
- Tendances des Applications Mathématiques en Tunisie, Algérie, Maroc 10-13 mai 2017, May 2017, Hammamet, Tunisia
- Accès au texte intégral et bibtex
-
Reports
- titre
- On the identification of multiple space dependent ionic parameters in cardiac electrophysiology modelling
- auteur
- Yassine Abidi, Mourad Bellassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- [Research Report] INRIA. 2017
- Accès au texte intégral et bibtex
-
Preprints, Working Papers, …
- titre
- Sensitivity of the electrocardiographic problem to multiple independent sources of uncertainty
- auteur
- Rajae Aboulaich, Najib Fikal, Emahdi El Guarmah, Nejib Zemzemi
- article
- 2017
- Accès au texte intégral et bibtex
-
2016
Journal articles
- titre
- Stochastic Finite Element Method for torso conductivity uncertainties quantification in electrocardiography inverse problem
- auteur
- Rajae Aboulaich, Najib Fikal, Emahdi El Guarmah, Nejib Zemzemi
- article
- Mathematical Modelling of Natural Phenomena, 2016, 11 (2), pp.1-19. ⟨10.1051/mmnp/201611201⟩
- Accès au texte intégral et bibtex
-
- titre
- Stability results for the parameter identification inverse problem in cardiac electrophysiology
- auteur
- Jamila Lassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- Inverse Problems, 2016, 32 (11), pp.1-31. ⟨10.1088/0266-5611/32/11/115002⟩
- Accès au texte intégral et bibtex
-
Conference papers
- titre
- Sensitivity of the electrocardiographic forward problem to the heart potential measuement noise and conductivity uncertainties
- auteur
- Rajae Aboulaich, Najib Fikal, El Mahdi Guarmah, Nejib Zemzemi
- article
- Colloque africain sur la recherche en informatique et mathématiques appliquées, CARI 2016, Oct 2016, Hammamet, Tunisia
- Accès au texte intégral et bibtex
-
- titre
- Identification of sources for the bidomain equation using topological gradient
- auteur
- Jamila Lassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- Colloque africain sur la recherche en informatique et mathématiques appliquées, CARI 2016, Oct 2016, Hammamet, France
- Accès au texte intégral et bibtex
-
- titre
- A Nash-game approach to solve the Coupled problem of conductivity identification and data completion
- auteur
- Rabeb Chamekh, Abderrahmane Habbal, Moez Kallel, Nejib Zemzemi
- article
- PICOF (Problèmes Inverses, Contrôle et Optimisation de Formes), Jun 2016, Autrans, France
- Accès au texte intégral et bibtex
-
- titre
- Stability results for the parameter identification inverse problem in cardiac electrophysiology
- auteur
- Lassoued Jamila, Mahjoub Moncef, Nejib Zemzemi
- article
- PICOF (Problèmes Inverses, Contrôle et Optimisation de Formes), Jun 2016, Autrans, France
- Accès au bibtex
-
2015
Journal articles
- titre
- Stability analysis of the POD reduced order method for solving the bidomain model in cardiac electrophysiology
- auteur
- Cesare Corrado, Jamila Lassoued, Moncef Mahjoub, Nejib Zemzemi
- article
- Mathematical Biosciences, 2015, ⟨10.1016/j.mbs.2015.12.005⟩
- Accès au texte intégral et bibtex
-
Conference papers
- titre
- Accuracy of Lead Removal vs Linear Interpolation in Non-Invasive Electrocardiographic Imaging (ECGI)
- auteur
- Laura Bear, Mark Potse, Josselin Duchateau, Nejib Zemzemi, Yves Coudière, Rémi Dubois
- article
- Computing in cardiology, Sep 2015, Nice, France
- Accès au texte intégral et bibtex
-
- titre
- Inverse Localization of Ischemia in a 3D Realistic Geometry: A Level Set Approach
- auteur
- Carlos E. Chavez, Felipe Alonso-Atienza, Nejib Zemzemi, Yves Coudière, Diegó Alvarez
- article
- Computing in cardiology, Sep 2015, Nice, France
- Accès au texte intégral et bibtex
-
- titre
- Inverse problem in electrocardography via the factorization method of boundary value problems
- auteur
- Julien Bouyssier, Nejib Zemzemi, Jacques Henry
- article
- IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, Apr 2015, New York, France. ⟨10.1109/ISBI.2015.7163979⟩
- Accès au texte intégral et bibtex
-
Book sections
- titre
- Sensitivity of the Electrocardiography Inverse Solution to the Torso Conductivity Uncertainties
- auteur
- Nejib Zemzemi, Rajae Aboulaich, Najib Fikal, Emahdi El Guarmah
- article
- Hans van Assen; Peter Bovendeerd ; Tammo Delhaas. Functional Imaging and Modeling of the Heart, Lecture Notes in Computer Science (9126), Springer, pp.475-483, 2015, 8th International Conference, FIMH 2015, Maastricht, The Netherlands, June 25-27, 2015. Proceedings, 978-3-319-20308-9. ⟨10.1007/978-3-319-20309-6_54⟩
- Accès au texte intégral et bibtex
-
Poster communications
- titre
- Sensitivity of the electrocardiography inverse solution to the torso conductivity uncertainties
- auteur
- Rajae Aboulaich, Najib Fikal, El Mahdi El Guarmah, Nejib Zemzemi
- article
- LIRYC scientific day, Jun 2015, Pessac, France
- Accès au texte intégral et bibtex
-
- titre
- New Mathematical approaches in Electrocardiography Imaging inverse problem
- auteur
- Nejib Zemzemi, Mark Potse, Laura Bear, Yves Coudière, Rémi Dubois, Jacques Henry, C Dallet, Josselin Duchateau, O Bernus, M Haïssaguerre
- article
- LIRYC scientific day, Jun 2015, Pessac, France
- Accès au texte intégral et bibtex
-
Medical context
Atrial fibrillation (AF) is the most common sustained heart arrhythmia. Ventricular fibrillations (VF) are more dangerous and are responsible for sudden cardiac death.
The LIRYC institute is one of six French university hospital institutions created in 2011 as part of the ”investments for the future” program (”Investissements d’avenir”) to boost medical research and innovation.
This institute, headed by Professor Michel Haissaguerre with clinicians from the University Hospital of Bordeaux and basic scientist teams is devoted to understanding the mechanism of AF and VF and developing new approaches to treat these cardiac pathologies. Carmen is an Inria team that is involved in the LIRYC institute by offering the modeling and simulation component of the project. One of the most used interventions to prevent and/ or stop VF and AF is radio-frequency ablation. This intervention requires an accurate targeting of the substrate to be ablated. The recent non-invasive technology used in guiding medical doctors to target these substrates is based on an inverse electrical mapping technique also known as electrocardiographic imaging (ECGI). With this approach, potentials on the outer (epicardial) surface of the heart are computed from potentials measured on the body surface using information on the geometry of the heart and the 3D locations of measured potentials. This is exactly the data completion Cauchy problem for elliptic equations. An ECGI mapping system was approved for use in Europe in 2011 and is available for clinical and basic science research at the LIRYC Institute in Bordeaux.
In this context, we would like to create a the EPICARD project, and the goal is to implement and test different mathematical approaches solving the ECGI problem but also to invent and design new mathematical approaches to study the problem differently than what has been done in the literature. In particular, physiologically detailed model personalization has not been considered in the literature mainly because of the mathematical and numerical challenge that it raises.
The LIRYC institute is one of six French university hospital institutions created in 2011 as part of the ”investments for the future” program (”Investissements d’avenir”) to boost medical research and innovation.
This institute, headed by Professor Michel Haissaguerre with clinicians from the University Hospital of Bordeaux and basic scientist teams is devoted to understanding the mechanism of AF and VF and developing new approaches to treat these cardiac pathologies. Carmen is an Inria team that is involved in the LIRYC institute by offering the modeling and simulation component of the project. One of the most used interventions to prevent and/ or stop VF and AF is radio-frequency ablation. This intervention requires an accurate targeting of the substrate to be ablated. The recent non-invasive technology used in guiding medical doctors to target these substrates is based on an inverse electrical mapping technique also known as electrocardiographic imaging (ECGI). With this approach, potentials on the outer (epicardial) surface of the heart are computed from potentials measured on the body surface using information on the geometry of the heart and the 3D locations of measured potentials. This is exactly the data completion Cauchy problem for elliptic equations. An ECGI mapping system was approved for use in Europe in 2011 and is available for clinical and basic science research at the LIRYC Institute in Bordeaux.
In this context, we would like to create a the EPICARD project, and the goal is to implement and test different mathematical approaches solving the ECGI problem but also to invent and design new mathematical approaches to study the problem differently than what has been done in the literature. In particular, physiologically detailed model personalization has not been considered in the literature mainly because of the mathematical and numerical challenge that it raises.
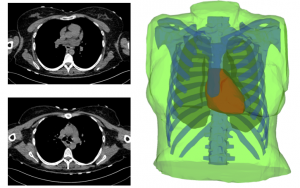
The ECGI procedure
One of the most recent heart imaging techniques introduced recently to the clinical industry is the electrocadiography imaging (ECGI). This technique allows a non-invasive reconstruction of the electrical potential on the heart surface based on the electrical potential measurement on the body surface and anatomical data of the torso. It has been a research topic for decades and it is now under clinical assessment in different leading hospitals around the world. ECGI provides very precious informations about the heart condition since it is able to provide refined spatial description of the electrical wave pathway and magnitude on the heart surface. This helps a lot in different clinical interventions like radio-frequency ablation usually used to stop atrial and ventricular arrhythmias. We work together with cardiologist from CHU de Bordeaux in order to improve the algorithm behind the inverse problem solving.
In order to solve the ECGI inverse problem many steps have to be taken into account: image segmentation, mesh generation, mathematical approaches, numerical algorithms and scientific visualization.
Image Segmentation and Mesh Generation
We use anathomical geometries provided by CHU de Bordeaux. Here is an exampmle of a CT scan of a 43 year old woman. We first segment the DICOM images, we identify the main regions in the torso domain: heart, lungs, bones, and the rest of the torso tissue. After segmentation, we use Tetgen MMG3D meshing Software in order to get a good quality of athetrahedral mesh.
Mathematical methods
The most widely used mathematical formulation used to solve ECGI inverse problem is a least square equation minimizing the gap between the measured ECGs and potentials mapped from the heart to the torso using a transfer matrix. This problem is ill posed since the transfer matrix it self could be a rectangular matrix. Many approaches have been used in the litterature to regularise the problem.
In this team project we aim to provide novel formulation of this inverse problem and compare them to the state-of-the-art procedure. We already have got promising results with the following methods:
In this team project we aim to provide novel formulation of this inverse problem and compare them to the state-of-the-art procedure. We already have got promising results with the following methods:
- Iterative Kozlov- Maz’ya-Fomin (KMF) method .
- A domain decomposition approach for solving the Inverse problem in electrocardiography .
- A Steklov-Poincaré Variational Formulation of the Inverse Problem in Cardiac Electrophysiology .
- A Machine Learning Technique Regularization of the Inverse Problem in Cardiac Electrophysiology .
- Factorization of boundary problems method for solving ECGI .
Our aim is to build a library that allows comparing these methods to the methods develepped by the project team members and other approches in the littterature.
Numerical Algorithms
Numerical algorithms are computer implementation of the mathematical methods on the computational geometries.
They have to be very acccurate but also sufficiently fast in order to be used in clinical applications
They have to be very acccurate but also sufficiently fast in order to be used in clinical applications
Visualization
Numerical algorithms provide tables with numbers. The interpretation of this data is difficult without a good representation.
Visualization tools, like paraview, help in representing this data with images and movies that medical doctors could easily interpret.
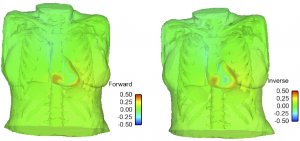
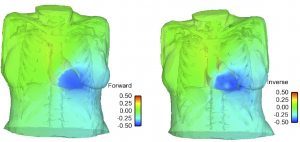
Example of normal case
Example of a re-entree case
Gallery of preliminary results
[youtubegallery]
[/youtubegallery]
[youtubegallery]
[/youtubegallery]
