BOOST develops and combines advanced mathematical and computational tools to model, analyze, and control human physiological and motor systems. Our work draws from control theory, signal processing, machine learning, and biomechanics to address challenges in health, movement, and human–machine interaction.
1. Mathematical Modeling
BOOST develops advanced mathematical models to describe the complex dynamics of human physiological systems, with the aim of inferring hidden states and personalizing health monitoring. These models serve as a foundation for understanding and predicting system responses, guiding decision-making in personalized training and treatment strategies. We focus on capturing features such as nonlinearities, delays, multi-scale behaviors, and uncertainties that are inherent to biological systems.
To address these challenges, we explore a wide range of modeling approaches, including nonlinear ODEs, PDEs, and non-local formulations like fractional or integral operators, as well as stochastic models. The models are tailored to specific applications and calibrated using physiological data, enabling the design of bio-informed feedback systems that can monitor and optimize individual performance and well-being.
2. Hybrid Estimation Methods
We focus on developing robust estimation frameworks for complex physiological models. A key emphasis of our work is on hybrid approaches that integrate classical observer theory—such as asymptotic and non-asymptotic observers—with modern learning-based techniques, including machine learning and data-driven inference. This synergy allows us to leverage the strengths of both domains: the interpretability and stability guarantees of traditional control theory, and the adaptability and generalization capabilities of data-driven methods. These hybrid estimators are particularly valuable in uncertain or real-world environments, where measurements may be noisy, incomplete, or affected by individual variability.
3. Control Strategies for Movement and Assistance
We design control strategies that combine model-based approaches like Model Predictive Control (MPC) with data-driven methods such as Reinforcement Learning (RL). This hybrid approach aims to leverage the robustness and constraint-handling of MPC with the adaptability and learning capabilities of RL. Applications include neuromechanical control, human–robot interaction, and personalized health interventions, where adaptive and intelligent feedback is essential under uncertainty.
In health contexts, we explore concepts like Dynamic Treatment Regimes (DTRs), where sequential decision rules adjust treatment based on patient status. This aligns naturally with RL frameworks and is promising for optimizing interventions in chronic disease management or sports performance. These hybrid control strategies offer robustness to uncertainty and personalization to individual needs, paving the way for smarter, adaptive, and effective control systems in health and human movement applications.
4. Signal Analysis
We develop a semi-classical signal analysis (SCSA), a unique method based on the spectral decomposition of the Schrödinger operator. Unlike traditional signal decomposition tools, SCSA expresses the signal through a set of squared eigenfunctions that depend directly on the signal itself. This data-adaptive basis captures detailed morphological variations, making SCSA especially suitable for physiological signals recorded continuously, such as arterial blood pressure or PPG signals. BOOST investigates both theoretical aspects—such as parameter tuning, eigenfunction properties, and quantum perturbation theory—and practical applications, including signal denoising, feature extraction, and 2D extensions for biomedical image enhancement.
BOOST Research Applications
1. Monitoring Athletes’ Stress
Understanding brain-body interactions to optimize performance and prevent overload.
Athletes are exposed to both mental and physical stress that can impair performance and affect long-term health. BOOST addresses this challenge by developing robust stress indicators using a multimodal approach that synchronizes neuro-psycho-physiological signals such as EEG, fNIRS, ECG, BP, and PPG, along with perceived stress metrics. These signals are analyzed through a combination of mathematical modeling, signal processing, and AI techniques to identify stress patterns and individual-specific responses. Our goal is to enable objective, real-time stress monitoring to support personalized training, recovery strategies, and well-being.
2. Prediction and Personalized Treatment of Vascular Diseases
Combining imaging, modeling, and AI for cardiovascular risk prevention.
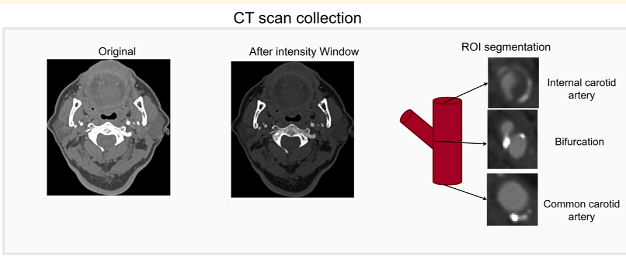
Vascular diseases are a major cause of morbidity and mortality worldwide, often progressing unnoticed until severe complications emerge. BOOST addresses this challenge by developing digital twin technologies that combine physical modeling, signal and image processing, and machine learning to monitor critical vascular risk factors such as arterial stiffness.
Our objective is to create non-invasive, interpretable diagnostic tools to assess vascular health in asymptomatic individuals, enabling earlier intervention and personalized treatment planning. Two key applications guide this research: the first focuses on diabetic foot prevention, where we model hemodynamic responses to detect early microvascular dysfunction; the second targets the assessment of vulnerable carotid plaques in asymptomatic patients to assist surgeons in making informed decisions about surgical interventions.
3. Bio-informed Closed-Loop Systems
Human–machine interaction powered by estimation and optimal control.
BOOST explores assistive movement technologies—such as robotic exoskeletons—that adapt in real-time to user needs. We tackle the challenge of designing intelligent control systems that combine model-based knowledge of human neuromechanics with machine learning strategies. By generating synthetic human-like motion data and learning its structure offline, we can reduce the need for extensive real-world demonstrations, making real-time control feasible.
Our work includes trajectory-based and trajectory-free control approaches, depending on whether future motion can be anticipated or must be inferred from physiological signals like EMG or joint torques. We leverage tools such as probabilistic movement primitives, differential game theory, and human-in-the-loop optimization. These enable personalized, adaptive controllers tailored for rehabilitation, sports training, or worker assistance. The human-robot interaction forms a biofeedback loop that responds dynamically to the user’s state, whether measured via fatigue, force, or neural signals.
Wearable Signals for Health and Performance Monitoring
From fatigue detection to injury prevention — real-time insights from the body.
BOOST places a strong emphasis on the use of wearable devices as essential tools for continuous health and performance monitoring. These devices, such as photoplethysmography (PPG), allow for non-invasive, real-time tracking of physiological and biomechanical signals in both controlled and natural environments. Wearable devices offer a non-invasive, portable, and scalable way to assess health, track performance, and prevent injury. By analyzing real-time data streams through machine learning and model-based techniques, we aim to extract meaningful indicators of fatigue, stress, injury…