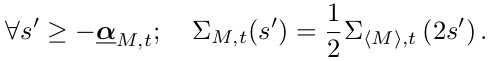The simplest and most popular measures of local regularity are the pointwise and local Hölder exponents.
For a stochastic process {X(t)}t∈R whose trajectories are continuous and nowhere differentiable, these are defined, at a point t0, as the random variables:
The pointwise Hölder exponent is a very versatile tool, in the sense that the set of pointwise Hölder functions of continuous functions coincides with the set of lower limits of sequences of continuous functions. In this sense, the pointwise exponent is often a more precise tool than the local one, since local Hölder functions are always lower semi-continuous. This is why, in particular, the exponent is used as a basis ingredient in multifractal analysis.
For certain classes of stochastic processes, and most notably Gaussian processes, it has the remarkable property that, at each point, it assumes an almost sure value.
Obviously, neither exponent gives a complete description of local regularity, even for continuous processes. The pointwise exponent is for instance insensitive to “oscillations”, contrarily to the local exponent: at 0, the function x^a*sin(x^(-b)), where a and b are positive real numbers, has pointwise exponent a, but local exponent a/(1+b).
Another, related, drawback of the pointwise exponent is that it is not stable under integro-differentiation, which sometimes makes its use complicated in applications. Again, the local exponent provides here a useful complement since it is stable under integro-differentiation.
Both exponents are useful in various applications including image processing, financial data analysis and the study of biomedical signals.
A much more complete description of the local regularity is given by 2-microlocal analysis: a function f is said to belong to the 2-microlocal space Cs,s’ (x0), where s + s’ > 0, s’ < 0, if and only if its m = [s + s’]-th order derivative exists around x0, and if there exists d > 0, a polynomial P with degree lower than [s]-m, and a constant C, such that :
These spaces are stable through integro-differentiation, i.e. f∈Cs,s’ (x0), if and only if f’∈Cs-1,s’ (x0).
For Gaussian processes, we have proved that it is possible to characterize, in an almost sure way, to which 2-microlocal spaces a given process belongs from conditions on its incremental variance. Upper Bounds are available for general processes [1].
Related to the 2-microlocal frontier, the concept of pseudo 2-microlocal frontier has been introduced in [1] and developed in [2]. The main difference between these two tools lay in the fact that the pseudo frontier takes into account the polynomial component of a function where the usual one does not. More precisely, it is proved in [2] that classic and pseudo 2-microlocal frontiers satisfy
where the coefficient pf,t0 is defined by
The pseudo 2-microlocal frontier allows to completely characterize the regularity of a continuous local martingale M using its quadratic variation . Hence, we have shown in [2] that M satisfies
This result also extends the property obtained in [1] on the Wiener integral. Indeed, any classic stochastic integral is itself a local martingale, and therefore, the previous formula induces a characterization of the regularity of such processes. These tools are also prove to be useful in the study of the fine local regularity of solutions of stochastic differential equations. Different examples such as square of Bessel processes are studied in [2].
On-going work in our team deals with:
- analysing the 2-microlocal behaviour of Lévy processes and multifractional processes;
- performing the 2-microlocal analysis of certain simple self-regulating and multistable processes
- studying SDE that are of common use in areas such as finance or biology.
References:
[1] E. Herbin, J. Lévy Vehel. Stochastic 2-microlocal analysis. Stochastic Processes and their Applications, 2009.
[2] P. Balança, E. Herbin. 2-microlocal analysis of martingales and stochastic integrals. Stochastic Processes and their Applications, 2012.